Você lembra como resolver 720 ÷ 2 ÷ 3? A maioria já esqueceu

O tema da divisão sucessiva ainda causa dúvidas em muitos estudantes, principalmente quando aparecem números grandes ou expressões com várias divisões seguidas. Muitas vezes, a dificuldade não está só em fazer a conta, mas em entender o que realmente significa dividir por mais de um número, um depois do outro. Por isso, esse tipo de exercício é muito usado para treinar e reforçar ideias básicas de matemática do dia a dia, especialmente quando envolve frações e simplificações.

O que significa fazer divisões sucessivas com 720?

Quando aparece uma expressão como 720 ÷ 2 ÷ 3, a forma correta de ler é: primeiro, divide por 2; depois, divide o resultado por 3. Em linguagem matemática, isso pode ser escrito assim: (720 ÷ 2) ÷ 3, respeitando sempre a ordem em que as operações aparecem, da esquerda para a direita.

Apesar de a divisão não permitir trocar os números de lugar, podemos enxergar a mesma conta como uma única divisão. Em vez de dividir 720 por 2 e depois por 3, pensamos que estamos dividindo 720 por um número que representa o efeito conjunto desses divisores, obtido multiplicando 2 × 3, ou seja, 6.

Como calcular 720 ÷ 2 ÷ 3 passo a passo?

A expressão 720 ÷ 2 ÷ 3 pode ser resolvida seguindo exatamente a ordem em que aparece. Primeiro, fazemos 720 ÷ 2, o que dá 360. Em seguida, pegamos esse resultado (360) e dividimos por 3, obtendo 360 ÷ 3 = 120, que é o resultado final.

Outro jeito de resolver é agrupando os divisores. Nesse raciocínio, percebemos que dividir por 2 e depois por 3 é igual a dividir por 6, já que 2 × 3 = 6. Assim, substituímos a expressão por 720 ÷ 6, que também resulta em 120, mostrando que as duas formas são equivalentes.

• 720 ÷ 2 = 360
• 360 ÷ 3 = 120
• 720 ÷ (2 × 3) = 720 ÷ 6 = 120

Por que dividir por 2 e depois por 3 é o mesmo que dividir por 6?

Quando fazemos divisões sucessivas por números inteiros, como 2 e 3, estamos reduzindo o número original em etapas. Agrupar esses divisores significa encontrar um único número que produza o mesmo efeito, o que é possível porque 720 ÷ 2 ÷ 3 e 720 ÷ (2 × 3) representam a mesma operação final.

Isso acontece porque dividir por 2 e depois por 3 é o mesmo que dividir por 2 × 3. Em termos de frações, 720 ÷ 2 ÷ 3 pode ser visto como 720 × 1/2 × 1/3, o que equivale a 720 × 1/6. Assim, o efeito combinado das duas divisões é igual ao de uma única divisão por 6.

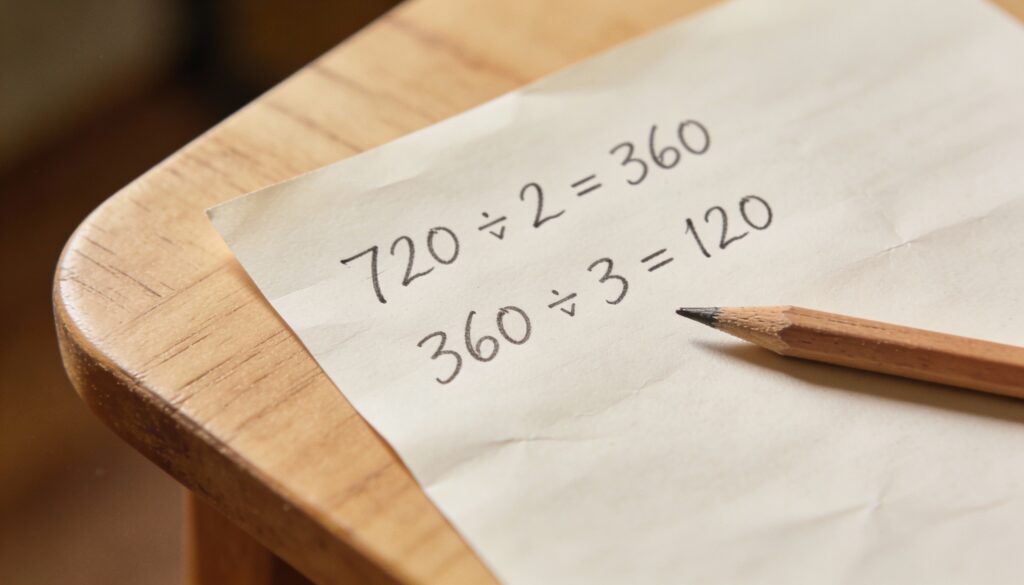
Por que transformar divisão em multiplicação pelo inverso?

Em muitos cálculos, principalmente com frações, é comum trocar uma divisão por uma multiplicação usando o inverso do número. O inverso de um número é aquele que, quando multiplicado por ele, resulta em 1; por exemplo, o inverso de 6 é 1/6, pois 6 × 1/6 = 1, o que torna a conta mais organizada.

No caso de 720 ÷ 6, podemos escrever 720 × 1/6, passando de uma divisão para uma multiplicação por fração. Em seguida, escrevemos tudo como fração, 720/6, e simplificamos para chegar a 120. Esse mesmo tipo de raciocínio ajuda em contas maiores, com várias divisões e frações em sequência.

• 720 ÷ 6 = 720 × 1/6
• 720 × 1/6 = 720/6
• 720/6 = 120, após simplificação

Quais cuidados ajudam a organizar divisões sucessivas?

Para quem está treinando esse tipo de cálculo, alguns cuidados simples tornam tudo mais claro. Eles ajudam a evitar erros comuns, como inverter a ordem das divisões, esquecer fatores ou se perder em contas muito longas, sobretudo quando envolvem frações e múltiplos divisores.

Nessa hora, vale a pena seguir algumas orientações práticas, que funcionam tanto para expressões simples, como 720 ÷ 2 ÷ 3, quanto para contas mais extensas, com vários números e parênteses.

Nunca foi tão fácil ficar bem informado com O Antagonista

Inscreva-se